WHU特供概率论第六章复习材料
数理统计
P149:4,6,7
P178:2:(2)(3)
总体与样本
定义 被研究的对象的全体称为总体
定义 组成总体的每个元素称为是个体
注 对每个个体而言,人们关心的往往只是个体的某个或某几个数量指标以及该指标在总体中的概率分布情况。
所谓总体,就是一个具有确定分布的随机变量。用随机变量X 或其分布函数F(x) 来表征总体,记作“总体X或“总体F(x)”总体X 的分布函数F(x) 在一般情况下是未知的,统计推断的任务就是确定总体的分布往往从总体中抽取一部分个体进行试验,通过试验获取定的数据,然后再利用这些数据来分析推断总体F(x)的具体分布形式。
定义 设(Xi,X,…,X) 是n 维随机变量,若X1,X,…,X,是相互独立的且与总体X 具有相同的分布,则称(Xi,X2,.·,X)是取自总体X 的容量为n 的简单随机样本,简称为样本
对抽取的n个个体进行试验,当试验全部完成后,就得到一组实数x1,x2,··xn,它们依次是X1,X2,…Xn。的观察值称(x1,x2,··,xn)是样本观察值或样本值。
统计量与抽样分布
定义 设(X1,X2,…,X,) 是来自总体的样本,g(xi,x2,…)是x1,x2,.·,xn 的连续函数,若g 不含任何未知参数,则称g(Xi,X2,…,X) 是统计量; 若(xi,2,…,x) 是样本观察值,则称g(xi,x,…·,x) 是该统计量的观察值
一些定义
若假设X1,X2,⋯,Xn是来自总体X的样本,x1,x2,⋯,xn为样本观察值
称统计量
- X=n1∑i=1nXi 样本平均值
- S2=n−11∑i=1n(Xi−X)2=n−11(∑i=1nXi2−nX2) 样本方差
- S=S2=n−11∑i=1n(Xi−X)2 样本标准差
- Ak=n1∑i=1nXik,k=1,2,⋯ 样本k阶距
- Bk=n1∑i=1n(Xi−X)k,k=1,2,⋯ 样本k阶中心距
上述统计量的观察值分别为
x=n1i=1∑nxi, s2=n−11i=1∑n(xi−x)2,s=s2=n−11i=1∑n(xi−x)2,ak=n1i=1∑nxik,bk=n1i=1∑n(xi−x)k,k=1,2,⋯
定理
设总体x 的数学期望和方差存在,并设
EX=μ,D(X)=σ2.
若(X1,X2,⋯,Xn) 是来自总体的样本,则有
E(X)=μ,D(X)=nσ2,E(S2)=σ2.
几个分布
统计量的分布称为抽样分布。在总体分布已知时,有时需要 一般情况下,确定统计量的分布是较困难的。但是当总体X 服从正态分布时,可求出x,S2 等统计量的精确分布。
x2分布
定义 设随机变量x1,x2,⋯,xn 相互独立且均服从标准正态分布N(0,1),则称随机变量
χ2=X12+X22+⋯+Xn2
服从自由度为n 的χ2 分布,记作χ2∼χ2(n)。
χ2(n) 分布的概率密度函数为
f(x)={22nΓ(2n)1x2n−1e−2x,0,当x>0,当x≤0.
χ2分布的独立可加性: 设ξ1∼χ2(n1),ξ2∼χ2(n2),且ξ1 与ξ2 相互独立,ξ1+ξ2∼χ2(n1+n2)
小结论
对xi~N(0,1)
E(χ2)=n,D(χ2)=2n
另外有正态分布的独立可加性
若Xi∼N(0,1)X1+X2+X3∼N(0,3)
对来自满足N(μ,σ2)整体的样本X1,X2…Xn
∑EXi2=nμ2+nσ2
例题
(1)设样本X1,X2,...,X。来自总体 N(0,1),Y=(X1+X2+X3)2+ (X4+X5+X6)2,试确定常数 C 使CY 服从x2分布.
(1) 因X1,X2,...,X6 是总体 N(0,1)的样本,故
x1+x2+x3 ~N(0,3),x4+x5+x6 ~$N( 0, 3) , $
且两者相互独立.因此
3x1+x2+x3∼N(0,1),3x4+x5+x6∼N(0,1),
且两者相互独立.按χ2分布的定义
3(X1+X2+X3)2+3(X4+X5+X6)2∼χ2(2),
即31Y∼˙χ2(2),即知C=31.
t分布
定义 设X∼N(0,1),Y∼χ2(n),且x 与Y 相互独立,则称随机变量
T=nYx
服从自由度为n 的t 分布,记作T∼t(n)。

注 当n 充分大时,自由度为n 的t 分布可近似地看成标准正态分布。
例题

(2) 因X1,X2,...,Xs 是总体 N(0,1)的样本,故X1+X2∼N(0,2),即有
2X1+X2∼N(0,1).
而
X32+X42+X52∼χ2(3).
且2X1+X2与X32+X42+X52相互独立,于是
(X32+X42+X52)/3(X1+X2)/2=23(X32+X42+X52)1/2X1+X2∼t(3),
因此所求的常数C=23.
F分布
定义 设随机变量X∼χ2(n1),Y∼χ2(n2),且x 与Y 相互独立,则称
F=n2Yn1X
服从自由度为n1,n2 的F 分布,记作F∼F(n1,n2)。
若F∼F(n1,n2),则F1∼F(n2,n1)
若T∼t(n),则T2∼F(1,n)
E(F(n1,n2))=n2−2n2
例题
(3) 已知总体 X∼t(n) ,求证 X2∼F(1,n).
(3)按定义总体X∼t(n),故X可表示成x=Y/nZ,
其中,Y∼χ2(n),Z∼N(0,1)且Z与Y相互独立,从而
xz=Y/nZ2.
由于Z∼N(0,1),Z∼χ2(1),上式右端分子Z2∼χ2(1),分母中Y∼χ2(n),又由Z 与Y相互独立,知Z2 与Y相互独立.按F分布的定义得
X2∼F(1,n).
正太总体,X∼N(0,4),X1,X2,⋯,X15是来自总体X的样本,试求随机变量
Y=2(X112+⋯+X152)X12+X22+⋯+X102
所服从的分布
解,设41S12=(2X1)2+⋯+(2X10)2∼χ2(10)设41S22=(2X11)2+⋯+(2X15)622∼χ2(5)∴Y=2(X112+⋯+X152)X12+⋯+X102=41S22/541S12/10∼F(10,5)
α分位数
定义 设x 是一随机变量,若对给定的α(0<α<1),存在常数η1 使得
P(X≤η1)=α,
则称η1为X 的下α 分位数或下α 分位点; 若对给定的α(0<α<1),存在常数η2 使得
P(X≥η2)=α,
则称η2 为X 的上α 分位数或上α 分位点。

正态总体的抽样分布
假设总体X 服从正态分布N(μ,σ2),(X1,X2,⋯,Xn) 是取自总体的样本,
X=n1∑k=1nXk,S2=n−11∑i=1n(Xi−X)2 分别为样本均值和样本方差。
定理 若总体X∼N(μ,σ2), 则样本均值X∼N(μ,nσ2).
推论 若总体X∼N(μ,σ2),则nσ2X−μ∼N(0,1).
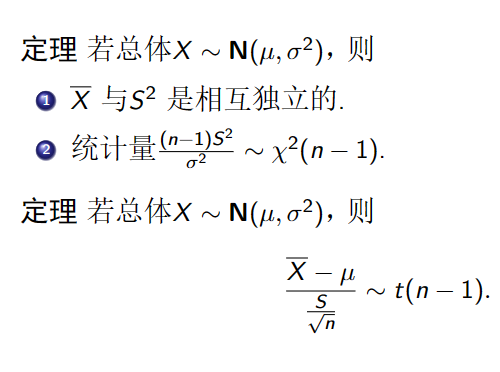
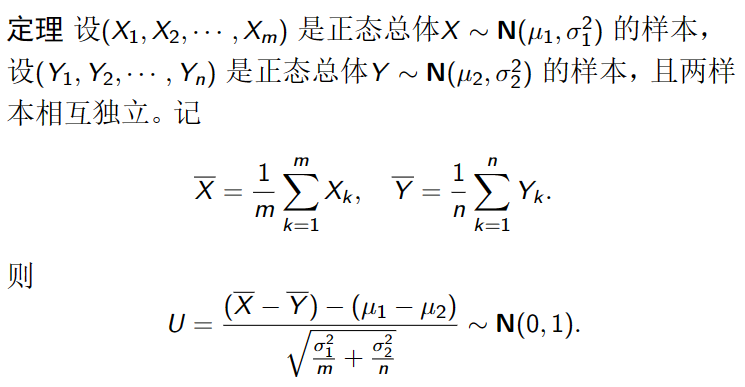
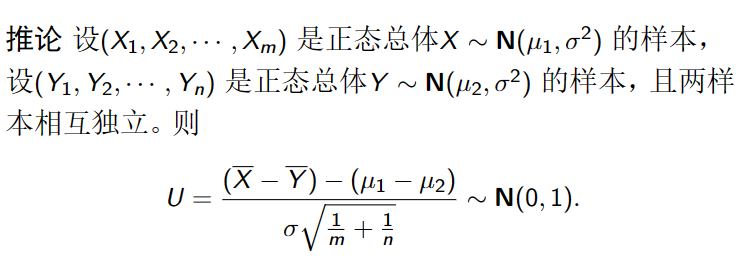


例题


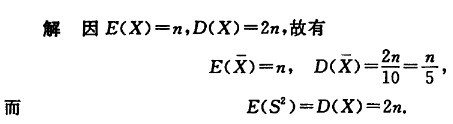



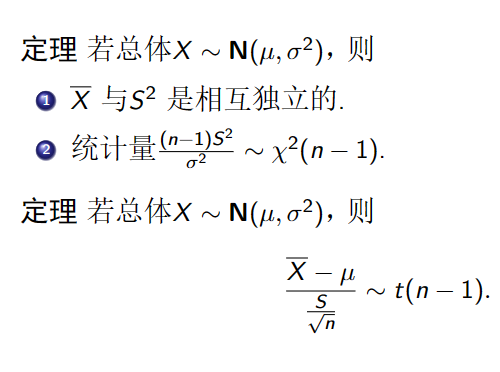




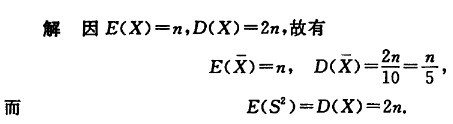


0 评论:
发表评论