极简离散数学元素和函数（part）

本篇文章将介绍离散数学中二元关系和函数的一些性质以及介绍一些例题。

二元关系

关系的表示

集合表示法、关系矩阵表示法、关系图表示法（一般只适合表示A的二元关系）

关系的性质

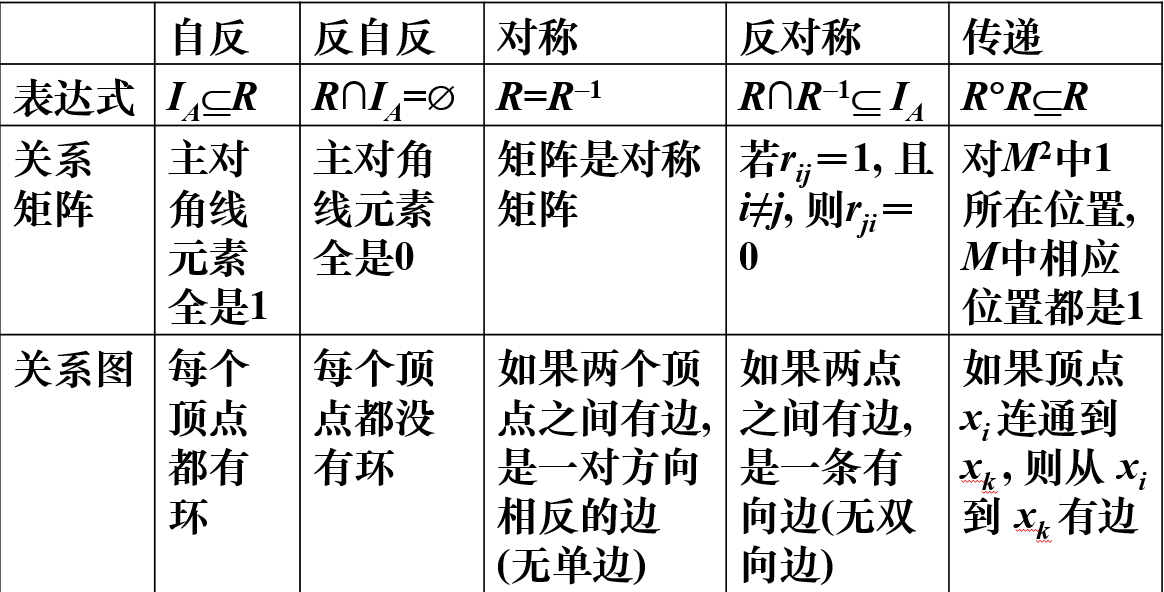
自反和反自反。
不具有自反性质的二元关系不一定具有反自反的性质。
关系图上看，反自反的图都无指向自己的环
对称，只具有 双向或者环。
反对称，节点间只有单向边。
传递。

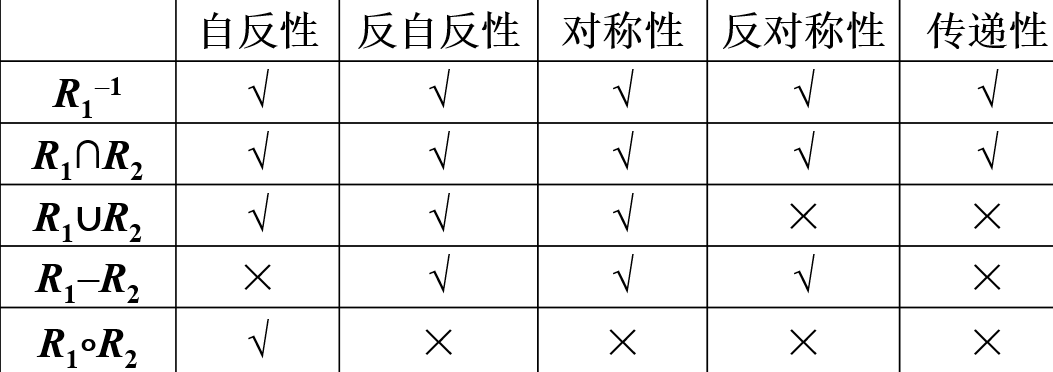
关系的逆

I上的小于关系的逆关系是大于关系。

关系的合成

具有结合律
对与和或具有分配律

关系的幂

定理 设A为n元集, R是A上的关系, 则存在自然数 s 和 t, 使得 $R^s = R^t$.

设$R$ 是$A$上的关系，若存在自然数 $s,t\left(s\leq t\right)$ 使得 $R^s=R^t$, 则
(1) $对任何k\in\text{ N有 }R^{s+k}=R^{t+k}$
(2) 对任何 $k,i\in\mathsf{N}$有 $R^{s+kp+i}=R^{s+i}$, 其中 $p=t$-s
(3) 令$S=\{R^0,R^1,...,R^{t-1}\}$,则对于任意的$q\in$N 有$R^q$$\in$S

计算有限集合上的关系的所有自然次幂的过程总会停止。
无限集合的自然次幂的过程不一定会停止。

关系的闭包

定义 设$R$是非空集合$A$上的关系，$R$的自反(对称或传递) 闭包是$A$上的关系$R^{\prime}$,使得$R^{\prime}$满足以下条件：

(1) $R^{\prime}$是自反的 (对称的或传递的)
(2) $R\subseteq R^{\prime}$
(3)对$A$上任何包含R的自反 (对称或传递) 关系$R^{\prime\prime}$有$R^{\prime}\subseteq R^{\prime\prime}.$
一般将 R 的自反闭包记作 $r(R)$, 对称闭包记作 $s(R)$, 传递闭包记作 $t(R).$

$$\left(1\right)r({R})=R\cup{R}^0$$

$$\left(2\right)s(R)=R\cup R^{-1}$$

$$(3)t(R)=R\cup R^2\cup R^3\cup...$$
设关系$R,r(R),s(R),t(R)$的关系矩阵分别为$M,M_r$, $M_s$和$M_t$,则

$M_r=M+E$
$M_s=M+M$
$M_t=M+M^2+M^3+...$

$E$ 是和$M$ 同阶的单位矩阵，$M'$是$M$ 的转置矩阵.
注意在上述等式中矩阵的元素相加时使用逻辑加.

设关系$R,r(R),s(R),t(R)$的关系图分别记为$G,G_r,G_s$, $G_t$, 则$G_r,G_s,G_t$的顶点集与$G$ 的顶点集相等.除了$G$ 的边以外，以下述方法添加新边：

考察$G$的每个顶点，如果没有环就加上一个环，最终得到$G_r$.考察$G$的每条边，如果有一条$x_i$到$x_j$的单向边，$i\#j$,则在$G$中加一条$x_i$到$x_i$的反方向边，最终得到$G_\mathrm{g}$. 考察$G$的每个顶点 $x_i$, 找从 $x_i$ 出发的每一条路径，如果从 $x_i$ 到路径中任何结点 $x_i$ 没有边，就加上这条边.当检查完所有的顶点后就得到图$G_t.$

(1) 若R是自反的, 则 s® 与 t® 也是自反的
(2) 若R是对称的, 则 r® 与 t® 也是对称的
(3) 若R是传递的, 则 r® 是传递的.

等价关系和划分

等价关系的定义与实例

设 R 为非空集合上的关系. 如果 R 是自反的、对称的和传递的, 则称 R 为 A 上的等价关系. 设 R 是一个等价关系, 若<x,y>∈R, 称 x 等价于y, 记做 x～y.

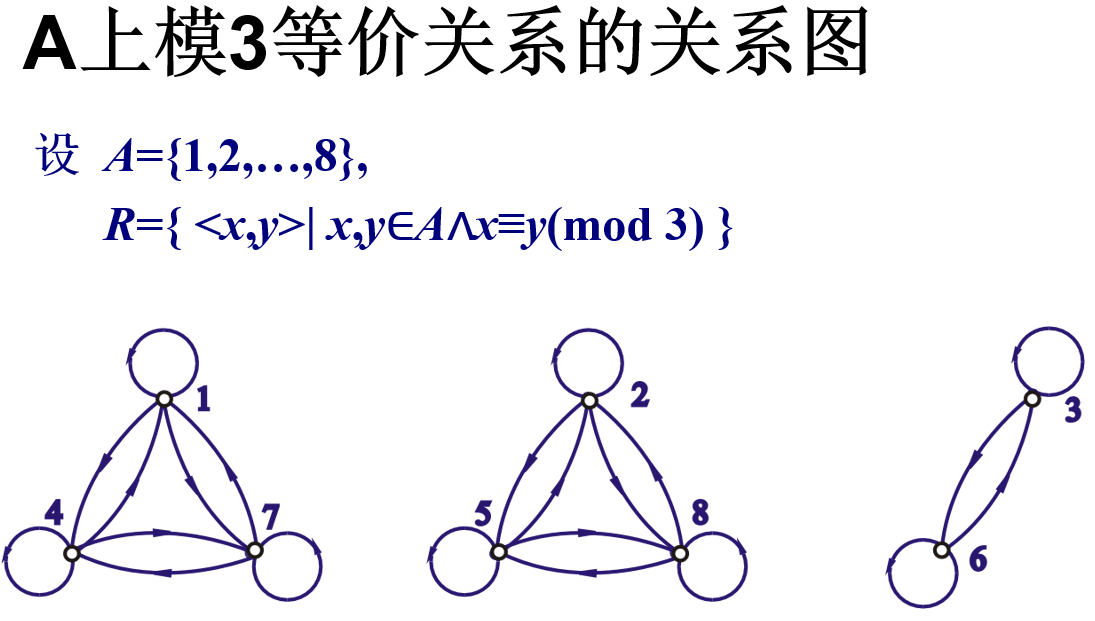
设 A={1,2,…,8}, 如下定义A上的关系 R：
R = { <x,y> | x,y∈A∧x≡y(mod 3) }
其中 x≡y(mod 3) 叫做 x 与 y 模3相等, 即 x 除以3的余数与 y 除以3的余数相等.

等价类及其性质

定义 设R为非空集合A上的等价关系, $\forall$x∈A，令
[x]R = { y | y∈A∧xRy }
称 [x]R 为 x 关于R 的等价类, 简称为 x 的等价类, 简记为[x].

实例 A={ 1, 2, … , 8 }上模 3 等价关系的等价类：
[1]=[4]=[7]={1,4,7}
[2]=[5]=[8]={2,5,8}
[3]=[6]={3,6}

商集与集合的划分

商集

设R为非空集合A上的等价关系, 以R的所有等价类作为元素的集合称为A关于R的商集,
记做A/R, A/R = { [x]$_R$ | x∈A }
A/R的每个成员之间不重合，并集为A
设$A \ne \varnothing$ ，R 是 A 上的等价关系，则商集A/R 是 A 的一个划分。
一个等价关系所诱导的划分是唯一的。
设 π 是非空集合 A 的划分，定义 A 上的二元关系 R 为aRb 当且仅当 a 和 b 同属于 A 的一个划分块。
则 R 是 A 上的等价关系。

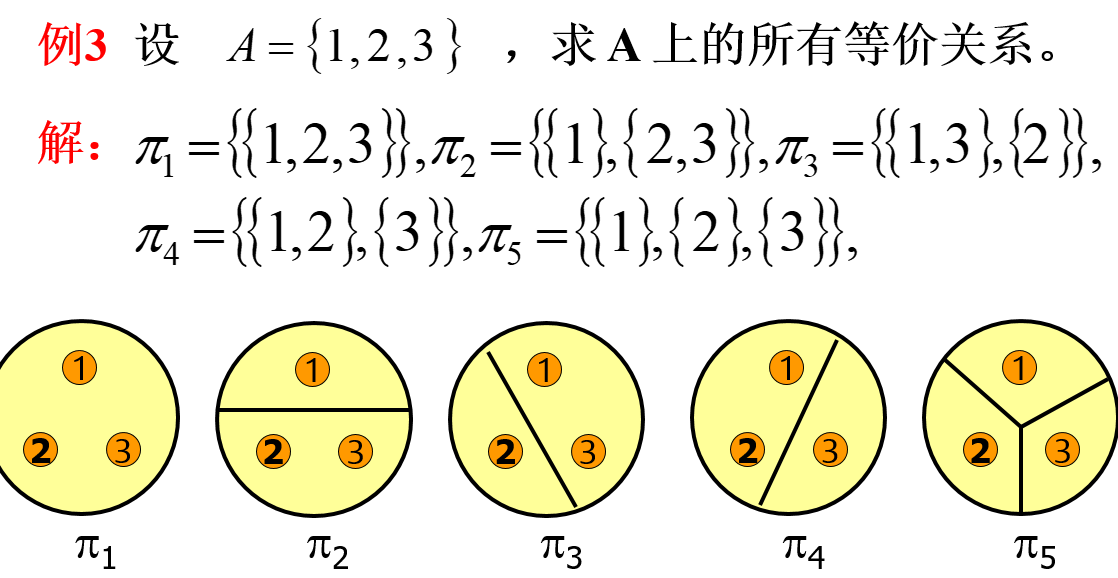
等价关系与划分的一一对应

一个等价关系可以唯一诱导出一个划分，一个划分也可以唯一诱导出一个等价关系。因此，可以通过求集合的划分来求一个集合上的等价关系。

例4 设 A={1, 2, 3, 4}，在 A$\times$A上定义二元关系R：
<<x,y>,<u,v>> $\in R \to$ x+y = u+v，
求 R 导出的划分.
根据 <x,y> 的 x + y = 2,3,4,5,6,7,8 将A$\times$A划分成7个等价类：
(A$\times$A)/R={ {<1,1>}, {<1,2>,<2,1>},

{<1,3>, <2,2>, <3,1>},

{<1,4>, <2,3>, <3,2>, <4,1>},

{<2,4>, <3,3>, <4,2>},

{<3,4>, <4,3>}, {<4,4>} }

偏序关系

x与 y 可比：设R为非空集合A上的偏序关系,
 x,y$\in$A, x与y可比 $\leftrightarrow$ x≼y ∨ y≼x.
全序关系：

R为非空集合A上的偏序, $\forall x,y\in A$, x与 y 都是可比的，则称 R 为全序（或 线序）

实例：数集上的小于或等于关系是全序关系(都具有这样的性质)
整除关系不是正整数集合上的全序关系(不是某数的整数倍就不是这条线上)

覆盖：设R为非空集合A上的偏序关系, x, y∈A, 如果 x ≺ y且不存在 z$\in$A 使得 x ≺ z ≺ y, 则称 y 覆盖x.
实例：{ 1, 2, 4, 6 }集合上的整除关系,
2 覆盖 1,
4 和 6 覆盖 2.
4 不覆盖 1.

偏序集与哈斯图

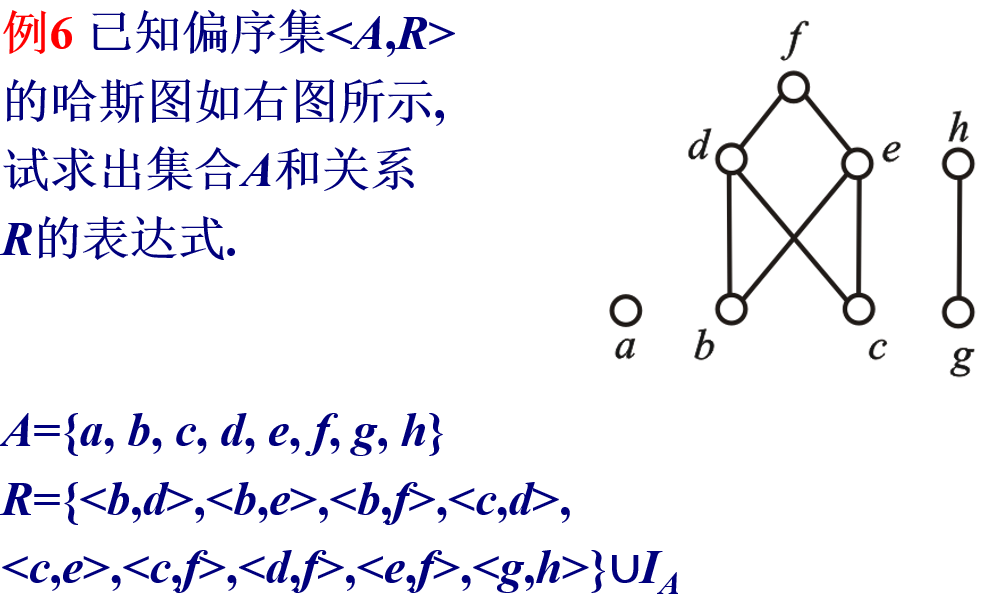
• 对于有穷集，极小元和极大元必存在，可能存在多个.
• 最小元和最大元不一定存在，如果存在一定惟一.
• 最小元一定是极小元；最大元一定是极大元.
• 孤立结点既是极小元，也是极大元.

• 下界、上界、下确界、上确界不一定存在

• 下界、上界存在不一定惟一

• 下确界、上确界如果存在，则惟一

• 集合的最小元就是它的下确界，最大元就是它的上确界；反之不对.

若有最大元/最大上届，那么唯一

函数

函数的定义

特殊的二元关系（更特殊的集合）

函数相等

一些概念

从A到B
设A, B为集合, 如果f 为函数
dom f = A ; ran f $\subseteq$ B,
则称 f 为从A到B的函数, 记作 f：A→B.

B上A
定义 所有从 A 到 B 的函数的集合记作 $B^A$,
读作“B上A”，符号化表示为
$B^A$ ={ f | f：A→B }

像
设函数 $f{:}A{\to}B,A{:}\subseteq A.$
1 $A_1$在$f$下的像： $f(A_1)=\{f(x)\mid x\in A_1\}$
函数的像$f(A)$
注意： 函数值 $f(x){\in}B$, 而像 $f(A_1){\subseteq}B.$

定义 设$f{:}A{\to}B{,}$
(1) 若ran$f=B$, 则称 $f{:}\quad A{\to}B$是满射的.
(2) 若 $\forall y \in$ran$f$ 都存在唯一的 x$\in$A使得 $f(x)=y$,则 称$f{:}A{\to}B$是单射的.
(3)若$f{:}A{\to}B$既是满射又是单射的，则称$f{:}$ $A\to B$是双射的

$f$满射意味着： $\forall y \in B$, 都存在 $x\in A$ 使得 $f(x)=y.$
$f$单射意味着： $f(x_1)=f(x_2)\Rightarrow x_1=x_2$