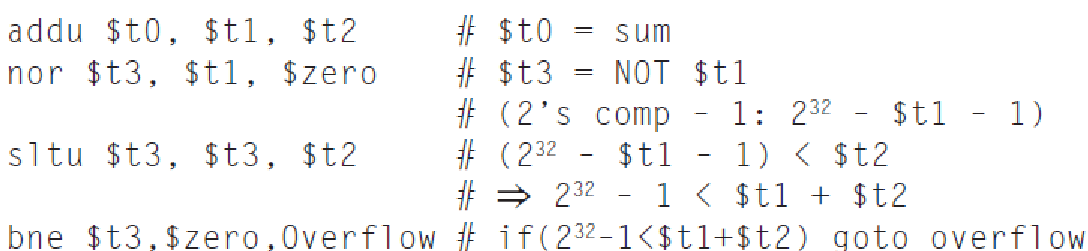计组06
补遗
浮点数小结
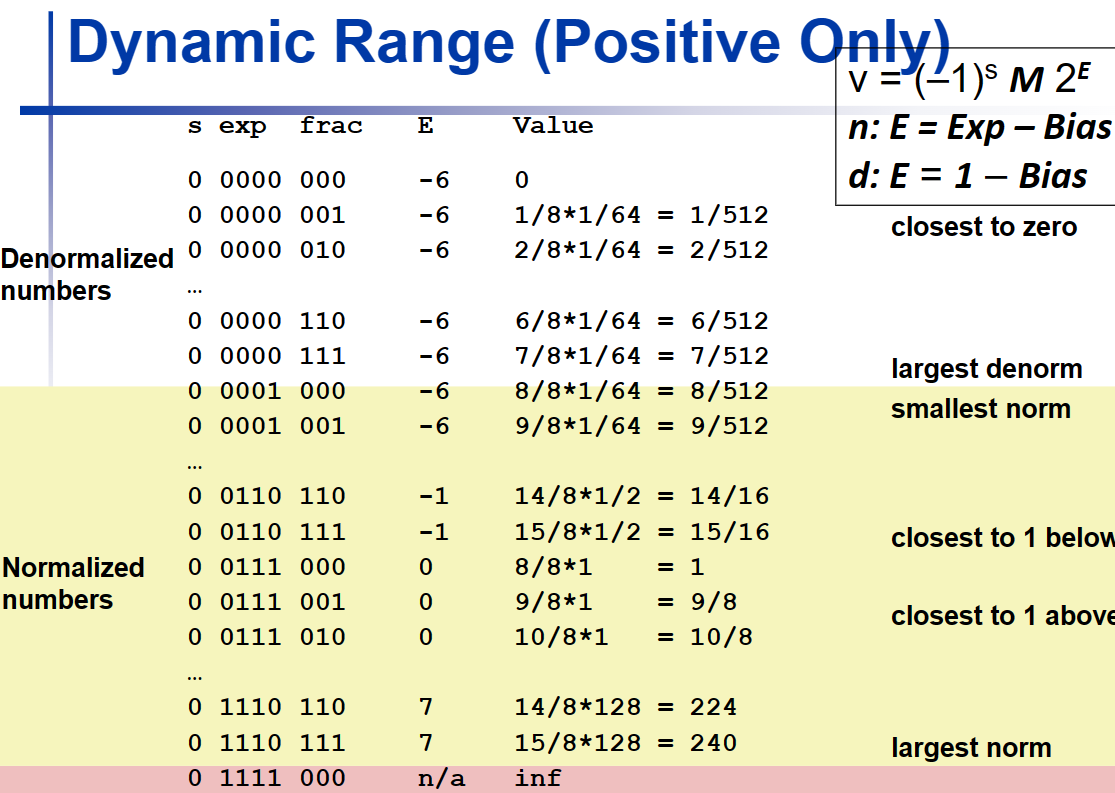
例如在 1 + 4 + 3中bias = 7浮点数 { 规格化浮点数 非规格化浮点数exp = 000...0 ( real exp = 1 − bias , M = 0. frac ) ± ∞ exp = 111...1 NaN frac ≠ 000.0 非数字编码
浮点数 \begin{cases}
规格化浮点数 \\
非规格化浮点数 \text{exp} = 000...0 \quad (\text{real exp} = 1-\text{bias}, M = 0.\text{frac})\\
\pm \infty \quad \text{exp} = 111...1\\
\text{NaN} \quad \text{frac} \ne 000.0 非数字编码
\end{cases}
浮点数 ⎩ ⎨ ⎧ 规格化浮点数 非规格化浮点数 exp = 000...0 ( real exp = 1 − bias , M = 0. frac ) ± ∞ exp = 111...1 NaN frac = 000.0 非数字编码 2 − 6 = 1 64 2^{-6} = \frac 1 {64} 2 − 6 = 64 1 用有效位用0.xxx 8 8 × 1 128 → 1 8 × 1 64 \frac 8 8 \times \frac 1 {128} \to \frac 1 8 \times \frac 1 {64} 8 8 × 128 1 → 8 1 × 64 1
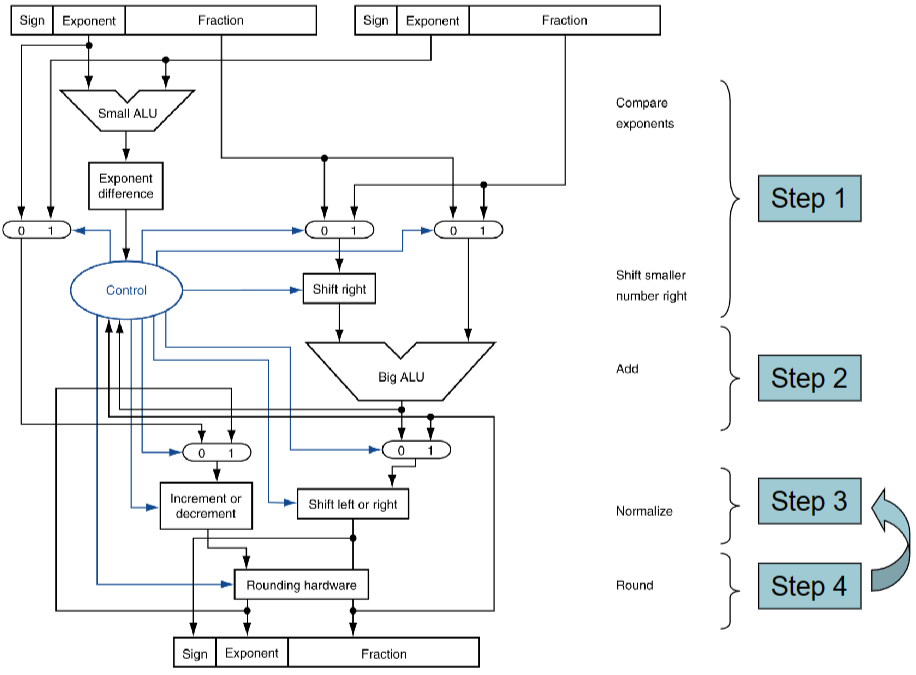
浮点数加法
先以DEC进制为例 9.999 × 1 0 1 9.999 \times 10^{1} 9.999 × 1 0 1 1.610 × 1 0 − 1 1.610 \times 10^{-1} 1.610 × 1 0 − 1
step
detail
1. 对阶,指数归一,小指数向大指数转化
0.0161 × 1 0 1 0.0161 \times 10^1 0.0161 × 1 0 1
2. 有效数位相加
10.015 × 1 0 1 10.015 \times 10^1 10.015 × 1 0 1
3. 规格化结果,检查溢出(指数)
$1.0015 \times 10^2 $
4. 舍入,向偶数舍入
→ 1.002 × 1 0 2 \to 1.002 \times 10^2 → 1.002 × 1 0 2
四舍六 入,中间值以下舍,中间值以上入,特判中间值,向偶数舍入
ori
approx
1.6
2
1.4
1
2.5
2
1.5
2
BIN中,例如取小数点后两位有效位.xx100
ori
approx
1.00101
1.01
1.00001
1.00
1.11100
10.00舍完后重新规整化
1.10100
1.10
这里0为偶数
这里流程设计加减
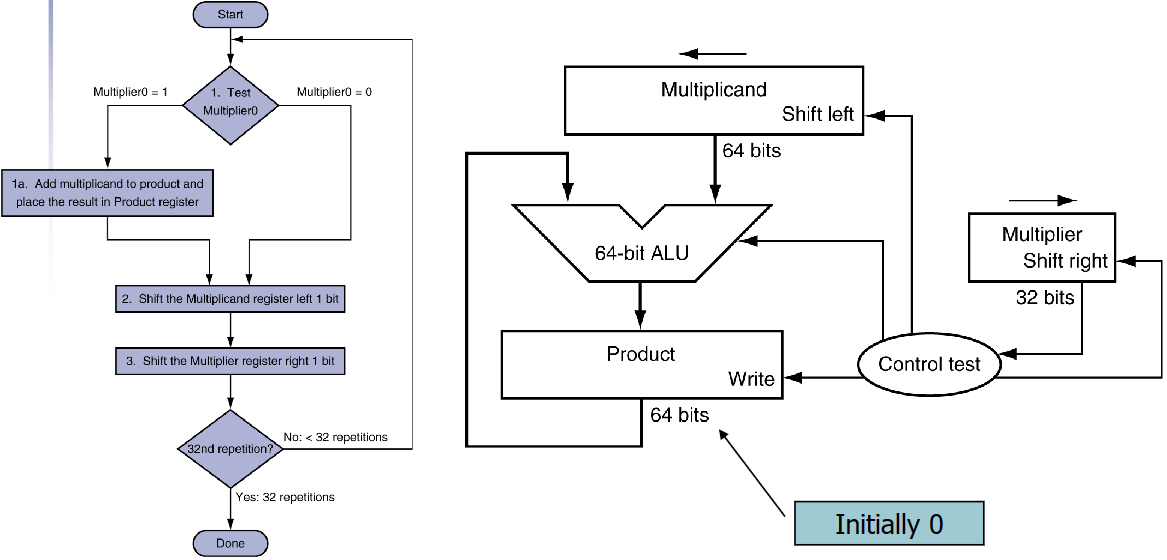
浮点数乘法
想想手工加法。
4bit两数相乘示例。
被乘数从右往左1stbit = 1, 这一位的积=乘数,| reg + cand = 1000
lier 2nd bit = 0 ,积为全0 | reg先右移1位,再+0 = 0100
lier 3rd bit = 0, 积为全0 | reg r shift ,再+0 = 0010
lier 4th bit = 1, 积=cand | reg r shift, result = 1001 000
再优化后 p13
mips 乘法,HI和LO
Two 32-bit registers for product
用法
mult rs,rt
multu rs,rt
64bit的结果存放在HI/LO
mfhi rd
mflo rd
load
mul rd,rs,rt
结果低32位赋值给rd
浮点数乘法
指数相加,有效数位相乘
除法
协处理器
FP instructions operate only on FP registers
lwcl ldcl swcl sdcl
ldcl $f8, 32($sp)
更多操作码add.s, sub.s, mul.s, div.s
◼ Double-precision arithmeticadd.d, sub.d, mul.d, div.d
◼ Single- and double-precision comparisonc.xx.s, c.xx.d (xx is eq, lt, le, ...)
◼ Branch on FP condition code true or falsebc1t, bc1f
代码示例
float f2c ( float fahr) {
return ( ( 5.0 / 9.0 ) * ( fahr - 32.0 ) ) ;
}
◼ fahr in $f12, result in $f0, literals in global memory space
f2c: lwc1 $f16, const5($gp)
lwc1 $f18, const9($gp)
div.s $f16, $f16, $f18
lwc1 $f18, const32($gp)
sub.s $f18, $f12, $f18
mul.s $f0, $f16, $f18
jr $ra
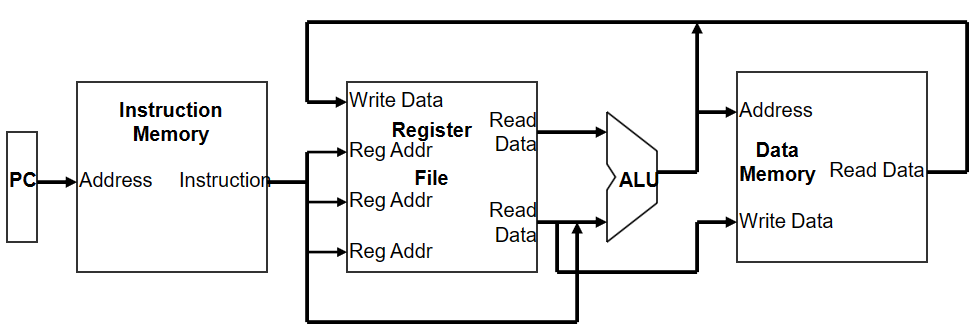
MIPS single cycle processor
C P U { 数据通路 { A L U ( 主要是整数 ) R F a n d M ( 高速缓存 ) 中央处理器
CPU \begin{cases} 数据通路 \begin{cases} ALU (主要是整数)\\
RF\ and\ M(高速缓存)
\end{cases}\\
中央处理器
\end{cases}
CP U ⎩ ⎨ ⎧ 数据通路 { A LU ( 主要是整数 ) RF an d M ( 高速缓存 ) 中央处理器
取指令,
PC → \to →
PC := PC + 4
执行指令
Two types of functional units:
elements that operate on data values (combinational)
elements that contain state (sequential)
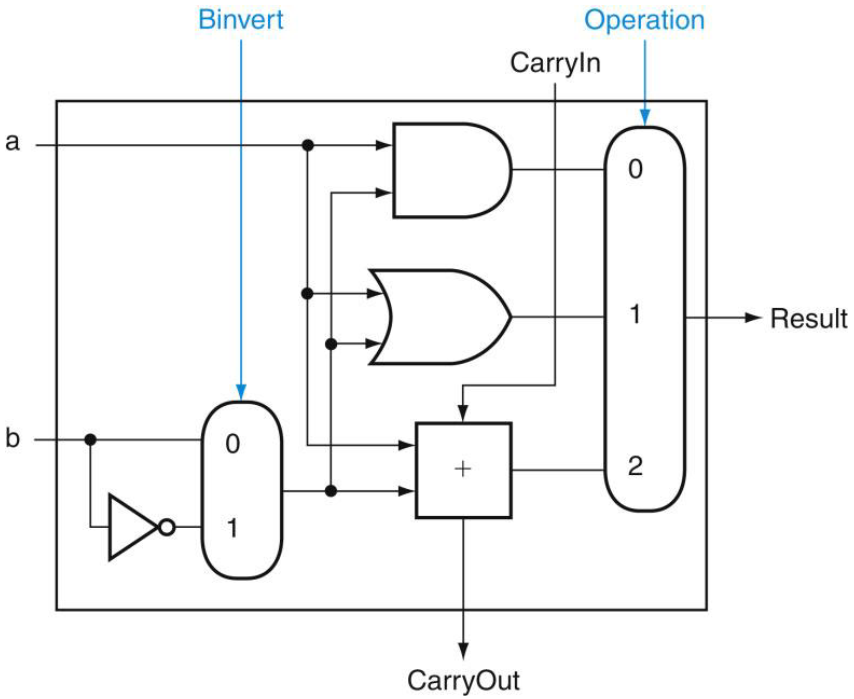
全加器,以及其执行的AND, OR, a + b, a + b ˉ \bar b b ˉ