宝箱

武汉大学网安计蒜客大一实训
这是附加题的最后一题
首先通过题目，树和遍历特殊边在每条边的情况很显然提示我们需要树形dp来解决这道题目。
树形 DP - OI Wiki

先考虑在不加入特殊边的情况下

在这里笔者用dp[i][k] 表示序号为i的节点的开宝箱状态为$k (k = 1 或 0)$时，将其作为根节点时的宝箱开法。
在叶子节点处可以选择开宝箱或者不开宝箱这两种状态，假设叶子节点的序号为$i$，用$1$表示开宝箱，用$0$表示不开宝箱那么满足
$$dp[i][0] = 1\\ dp[i][1] = 1$$
因为是叶子节点，所以开和不开都只有一种开法，就是他自己。
此时讨论这个叶子节点的父节点，因为题目没有说是二叉树，所以可能需要用图存储这个树来得到他的父节点序号，这里不讨论这些细节。假设这个叶子节点的父节点的序号是$r$，同时这个叶子节点还有$k-1$个兄弟节点，我们将他们统称为$s_i (i\in[0,k])$。

当父节点状态为1时，他的儿子们的状态可以为1也可以为0。
当父节点状态为0时，他的儿子们的状态只能为0。

因此这个父节点$r$的状态转移方程满足
$$dp[r][0] = \prod_{i=0}^k (dp[s_i][0] + dp[s_i][1]) \\ dp[r][1] = \prod_{i=0}^k (dp[s_i][0])$$

那么通过递归就可以很自然得到根节点宝箱开还是不开时的开法，而答案就是$dp[root][0] + dp[root][1]$

一些可能对接下来的讨论有帮助的结论

在讨论某父节点的状态时，如果父节点不选，状态为0，因为他的一个子节点$s_j$可能被特殊边影响我们计算父节点开法时不考虑这个特殊的子节点，那么
$$dp^{'}[r][0] = \frac {dp[r][0]}{dp[s_j][0] + dp[s_j][1]}$$

如果父节点选了，状态为1，那么去除他的特定儿子$s_j$后，开法种类为
$$dp^{'}[r][1] = \frac {dp[r][1]}{dp[s_j][0]}$$

其次考虑加入特殊边

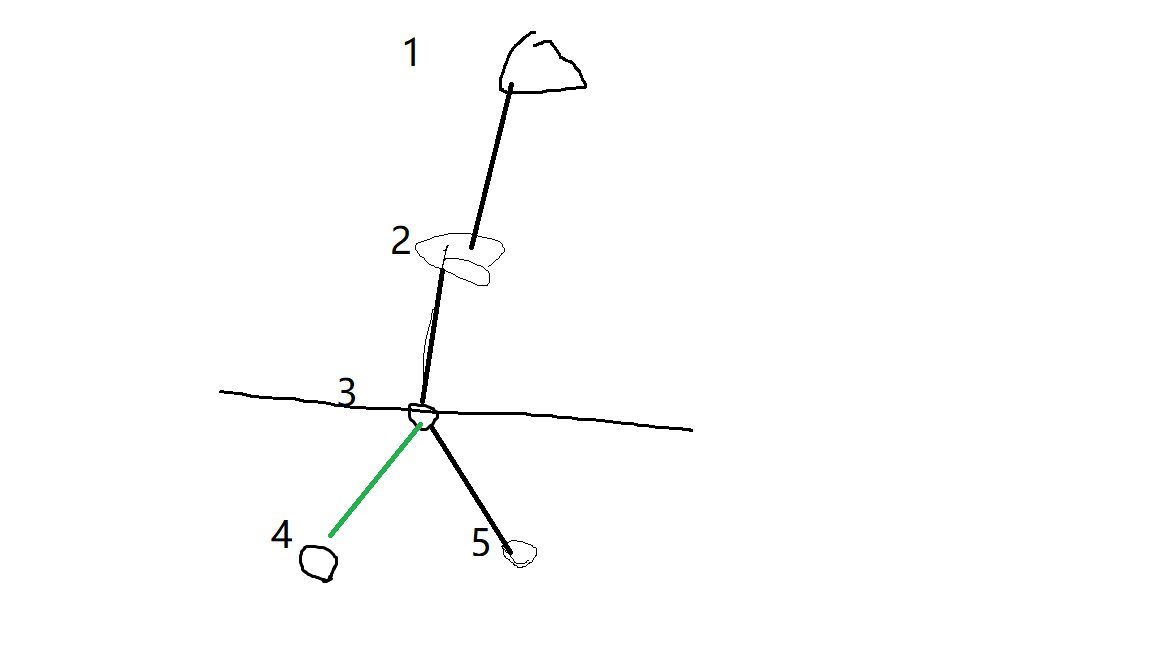
请看这张精湛细腻的图片，其中我们即将将特殊边放在3-4之间，此时3的另外一个儿子

这个特殊边很特殊，因为在其影响下的两个节点存在以下几种状态。我们需要将这三种情况得到的方法总数加起来

1. 父节点开，子节点不开
2. 父节点不开，子节点开
3. 父节点开，子节点开

但是3之上的2和1节点获得结果的公式不会因为3之下特殊边的更换而发生更换，众所周知，我们在树形dp的过程中，一个节点某状态的结果是这个节点的所有子节点某些状态（单个或和）的相乘的结果。换做通俗的话讲就是，上面的本意是好的，是你下面在搞特殊边，那么当你搞特殊化时，我把你当成临时工，把你开除就行了，你特殊计算，其他不受影响的仍按照之前的结果算出。
根据这种想法，所以我们引入一个新的二维数组base[i][k]来表示，序号为i所传达从根节点到i的一路上倍率公式。而对r的每个子节点s_i，有递推方程:
$$base[s_i][1] = base[r][0] \cdot \frac {dp[r][0]} {dp[s_i][0] + dp[s_i][1]}\\ \quad \\ base[s_i][0] = base[r][0] \cdot \frac {dp[r][0]} {dp[s_i][0] + dp[s_i][1]} + base[r][1] * \frac {dp[r][1]} {dp[s][0]}\\ \quad\\ 初始情况下base[1][0] = base[1][1] = 1$$

输出结果

至此我们就可以计算当某两个顶点受特殊边影响时的答案了。
若u,v受影响，其中u是v的父节点时：
$$ans_i =(dp[v][1] + dp[v][0]) \cdot (base[u][1] \cdot \frac {dp[u][1]} {dp[v][0]} ) + (base[u][0] \cdot \frac {dp[u][0]} {dp[v][0] + dp[v][1]} ) \cdot dp[v][1]$$
之后遍历每两个相邻树（共N个）就能得到结果了